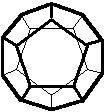
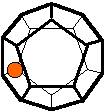
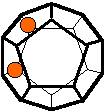
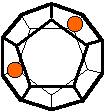
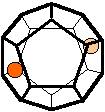
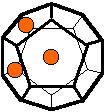
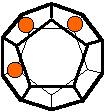
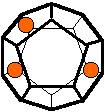
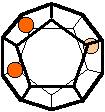
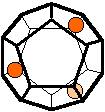
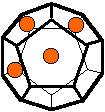
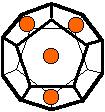
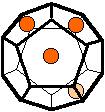
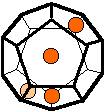
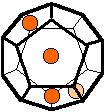
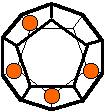
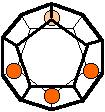
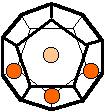
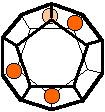
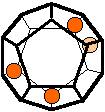
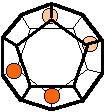
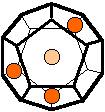
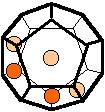
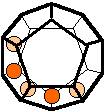
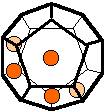
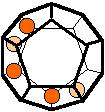
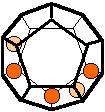
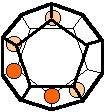
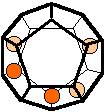
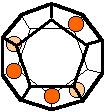
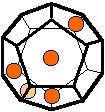
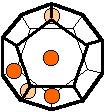
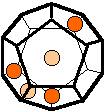
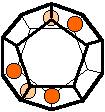
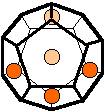
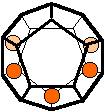
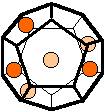
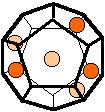
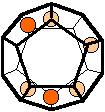
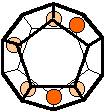
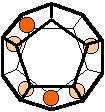
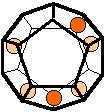
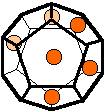
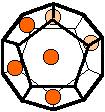
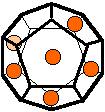
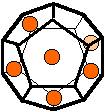
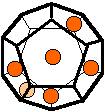
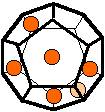
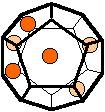
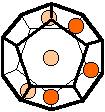
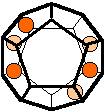
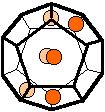
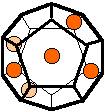
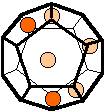
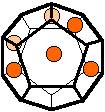
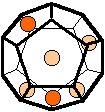
The 96 different colorings with two colors for the dodecahedra
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Shown are
only 60 patterns. The missing 36 patterns are the complements of the first 36
patterns with less than 6 colored sides. It is remarkable that in the 24
patterns with 6 colored sides a majority (the 12 magenta bordered assymetric
ones, ordered in pairs, and the 4 blue bordered symmetric ones) is equal to their
complement.
Complement
means exchanging colored and uncolored sides.
Counting 2
color patterns on the octahedra gives 23 and on the icosahedra 17’824.
Pink points are behind, the red ones in front.
See the Polya-Burnside Lemma for such countings!
The
Polya-Burnside-Formula for the 2-colored dodecahedron is
![]()